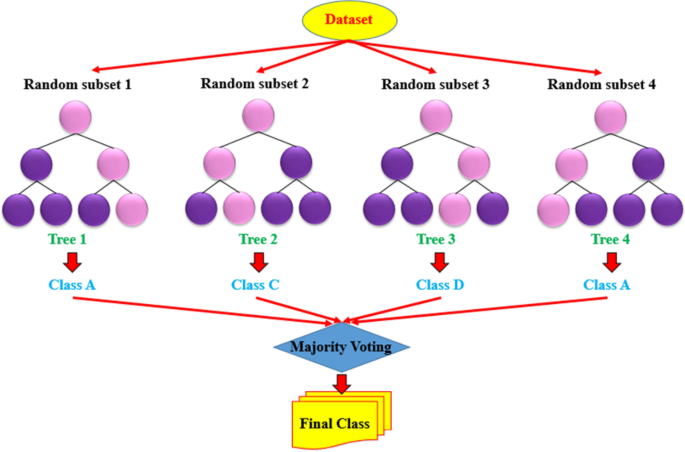
Modeling of CO2 adsorption capacity by porous metal organic frameworks using advanced decision tree-based models In recent years, metal organic frameworks (MOFs) have been distinguished as a very promising and efficient group of materials which can be used in carbon capture and storage (CCS) projects. In the present study, the potential ability of modern and powerful decision tree-based methods such as Categorical Boosting (CatBoost), Light Gradient Boosting Machine (LightGBM), Extreme Gradient Boosting (XGBoost), and Random Forest (RF) was investigated to predict carbon dioxide adsorption by 19 different MOFs. Reviewing the literature, a comprehensive databank was gathered including 1191 data points related to the adsorption capacity of different MOFs in various conditions. The inputs of the implemented models were selected as temperature (K), pressure (bar), specific surface area (m2/g) and pore volume (cm3/g) of the MOFs and the output was CO2 uptake capacity (mmol/g). Root mean square error (RMSE) values of 0.5682, 1.5712, 1.0853, and 1.9667 were obtained for XGBoost, CatBoost, LightGBM, and RF models, respectively. The sensitivity analysis showed that among all investigated parameters, only the temperature negatively impacts the CO2 adsorption capacity and the pressure and specific surface area of the MOFs had the most significant effects. Among all implemented models, the XGBoost was found to be the most trustable model. Moreover, this model showed well-fitting with experimental data in comparison with different isotherm models. The accurate prediction of CO2 adsorption capacity by MOFs using the XGBoost approach confirmed that it is capable of handling a wide range of data, cost-efficient and straightforward to apply in environmental applications. Carbon dioxide (CO2) plays a high influencing role in global warming1. As a result of consumption of fossil fuels especially in electricity generation, transportation and other industrial activities, CO2 emission into the atmosphere is surging2,3. According to an investigation by Pachauri et al. in 2014, carbon dioxide’s concentration in the atmosphere has increased from 280 to 400 ppm with 0.8 °C1,4. It is estimated that concentration of CO2 would touch a peak of 600–700 ppm at the dawn of 22th century and resultantly it will lead in 4.5–5 °C growth in the average temperature of earth5. Thus, as to put a halt on rapid growth of CO2 emission rates, United States Department of Energy (DOE) provided the world with a program aiming for reduction of CO2 concentrations by utilization of high efficiency CO2 capture plans. According to the issued program 90% of emitted CO2 could be captured just with less than 35% of additional budget allocation to carbon capture and storage (CCS) programs6. These programs could be contemplated as promising approaches for the separation and sequestration of CO2. As soon as carbon dioxide is separated, it could be stored underground, or alternatively it can be utilized in various industries such as oil industries in order to enhance the recovery7,8,9. Up to date, scientists have proposed numerous methods for CO2 capture among which absorption10,11,12, membranes13,14, and carbon-based adsorbents5,13 are well developed. Nevertheless; high total costs, low capacities, and challenging regeneration processes are some of their limitations15. A material which could be used successfully for an efficient CO2 capture process, not only should possess good characteristics for CO2 uptake, but also must release the captured carbon dioxide in the regeneration step. Furthermore, the effectiveness of the capturing process could be maximized provided that the structure of the material could be modified using various functional groups and molecular tuning approaches.Metal organic frameworks (MOFs) have been distinguished as a very promising and efficient group of materials which can be used in CCS projects because of their unique properties of being modifiable, stable in high temperatures, and having a chemical structure which can be easily adjusted16,17,18,19,20. Therefore, different advantages and disadvantages of MOFs have been investigated by several researchers such as an investigation done by Le et al., which reported how the architecture and active functional groups of MOFs could be controlled17. Moreover, having conducted various investigations on the thermal stability of MOFs, scientists have reported the impact of morphology and crystalline shape of these materials on their thermal stability21,22,23,24. Taking MOFs synthesized from strontium and calcium by the way of example, Yeh et al.25 found that, as a result of their micro-porosity, these materials were thermally stable in all temperatures lower than 450 °C. Some other scientific investigations have found that MOFs could be modified for various applications just by changing the functional groups, which are located on their pore walls26,27. It is wieldy known that MOFs are comprised of metal ions clusters and linkers which are organic molecules. These linkers have a 3D-structure of pores and connecting channels. While 3D-structurevoids adsorb molecules as their host, the primary structure of these materials provides reversible channels and pores as soon as desorption step take place26,27,28. Properties of MOFs is determined by the selected linker and the metal. For example, zinc in the structure of IRMOF-1 is the metal which is located at the center of structures and is connected to the terephthalic molecules. Having this structure, IRMOF-1 benefits from existence of pores with high capacity of adsorption. Furthermore, there are various groups of MOFs with their unique structures, properties and application. Some MOFs like UMCs have unsaturated metallic centers29, which provides carbon dioxide molecules with more active sites, hence facilitates formation of strong bonds between CO2 and the structure. Other advantage of MOFs in comparison to other materials like zeolite is that the MOFs have typically wider pores, which boost diffusion rate of molecules not only in a single structure, but also between different crystals30,31,32,33. That is why scientists believe that MOFs are promising for adsorption of CO2, emphasizing on their adjustable porosities and having a modifiable surface chemistry5,34,35,36. Regarding developing and testing MOF, there are some important challenges and obstacles to overcome or be solved using alternative methods. Firstly, experimental investigation of adsorption capacity of MOFs not only is time consuming, but also is not cost-effective. Secondly, data cannot be matched with the developed isotherms because typically these isotherms are proposed for a specific range of data31. So as to address the problem, many scientists have been trying to use soft computing methods by which not only the time and money could be saved, but also there is no need for simplifying assumptions and the data could be modeled more precisely. Artificial intelligence (AI) approaches are useful tools which enable us to estimate and develop representative models in various disciplines37,38,39,40,41,42. These powerful algorithms are able to model non-linear relationship which exist between influencing parameters. Up to the date, a plethora of models have been developed such as fuzzy logic, radial basis networks, support vector machine, and colony optimization43,44,45,46,47.In the current investigation, authors tried utilizing smart models for the prediction of nonlinear adsorption of CO2 by MOFs. According to the literature, scientists have done fewer researches on the modeling of CO2 adsorption by MOFs using AI methods. To model the CO2 uptake capacity of different MOFs, new and powerful methods of CatBoost, LightGBM, Random Forest (RF), and XGBoost were employed. CatBoost (which is the abbreviated form of categorical boosting) is an open-source and modern gradient boosting library and it can deal with problems which are intrinsically heterogeneous thought handling categorical features. XGboost and LightGBM belong to GBDTs (Gradient Boosted Decision Trees) and in these methods a tree structure includes two separate steps. Firstly, the appropriate structure for the tree must be found. Secondly, leaf values must be set as soon as the tree structure is finalized48. Another approach which was used in this investigation was Random Forest. Since it was introduced, the accuracy of classifications improved significantly because not only growth of various trees were allowed, but also the program is able to vote for best and most distinguished class49. Reviewing literature, the authors gathered 1191 data points related to the adsorption capacity of different MOFs at various temperatures and pressures. The investigated MOFs are ZIF-8, Zn-MOF-74, Mg-MOF-74, PCN-16, MOF-5, PCN-11, BeBTB, Co-BDP, Mg2(dobdc), Cu-BTTri, MOF-177, IRMOF-1, IRMOF-6, IRMOF-3, IRMOF-11, Cu-BTC, MOF-505, MOF-74, and MOF-250,51,52,53.In a tree-based ensemble method, a group of various classification and regression trees (CARTs) are utilized to minimize a set of objective functions applied to a training dataset. The XGBoost approach could be contemplated as a tree-based model which basically belongs to a gradient boosting decision tree (GBDT). So as to explain the CART’s basic structure, it is comprised of three various nodes namely (a) the main node (root node), (b) internal nodes, and (c) leaf nodes like as illustrated in Fig. 1. The binary decision-making processes will split the root node into internal nodes. Doing so, the dataset which is located in the root will be classified into various nodes in the internal nodes and the final classification will take place in the leaf nodes as the final classes. Aiming for developing a powerful set according to the gradient booting model, an ensemble of CATRs are introduced and developed using determination of their influence by giving them a specific weight during the training process54.Figure 1A schematic illustration of XGBoost depicting the main node, interior nodes, and the leaves.In a dataset where m dimension features and n examples exist, the modeling output (y) would be trained according to the following expression to form n tree nodes55:$$hat{y}_{i} = mathop sum limits_{k = 1}^{N} f_{k} left( {X_{i} } right), quad f_{k} in f$$$$where ; f = left{ {fleft( X right) = omega_{qleft( x right)} } right}, left( {q:m to T, omega in T} right)$$where a binary leaf index will be formed by mapping an example X using a defined decision rule q(x). In Eqs. (1) and (2), the corresponding space of each regression tree is depicted by ‘f’. Accordingly, fk represents the kth tree, tree leaves are denoted by T, and their corresponding weight is determined by ω.As the next step in the modeling, tree sets will be determined by minimizing an objective function denoted by L55:$$L = mathop sum limits_{i = 1}^{n} l(hat{y}_{i} ,y_{i} ) + mathop sum limits_{k = 1}^{N} {Omega }(f_{k} )$$$$with, {Omega }left( f right) = gamma T + frac{1}{2} lambda omega ^{2}$$In the given formulation, Ω represents the regularization function and limits the model complexity by reducing the overfitting issues; loss function is shown by l and intrinsically is a differentiable convex; the minimum loss is denoted by γ and it is necessary in division of a new ultimate class as a leaf, and λ stands for the regulation coefficient. γ and λ facilitates the growth of the variance of the model and resultantly plummet the overfitting issue55. Every leaf in the boosting model has its own objective function, which should be minimized iteratively as follows55:$$L^{left( t right)} = mathop sum limits_{i = 1}^{n} left{ {lleft( {y_{i} ,hat{y}_{i}^{{left( {t – 1} right)}} } right) + f_{t} left( {X_{i} } right)} right} + {Omega }left( {f_{t} } right)$$In the presented formula, t is the iteration number for the minimization of a leaf objective function in the training step. So as to improve the model, an algorithm known as the greedy algorithm is utilized, which is designed to provide enough space for regression trees. Doing so, XGBoost model can continuously update its final results through improving the preciseness of the objective functions55:$$hat{y}_{i}^{left( t right)} = hat{y}_{i}^{{left( {t – 1} right)}} + f_{t} left( {X_{i} } right)$$Shrinkage strategy is another strategy that XGBoost method utilizes properly. In this strategy, a learning factor is defined and its learning rate is regulated in every gradient boosting step through definition of additional weights. Shrinkage strategy prevents overfitting problem by restricting future trees from affecting previously formed trees56.Light gradient boosting machine (LightGBM)On the basis of gradient learning theories, a novel learning machine was developed which is known as LightGBM57. The LightGBM approach, in comparison to XGBoost, needs lower memory spaces and speeds up the training step by using a histogram58. LightGBM can form a histogram with a width of ‘k’ by discretizing eigenvalues into ‘k’ different bins. Furthermore, the aforementioned approach diminishes the need for a set of pre-sorted results and values will be saved in an integer with a size of eight bits, which results in a drastic reduction of memory consumption. That said, such as kind of approach unfortunately results in dipping the model’s preciseness. Leaf-wise approach has also been utilized in LightGBM. Drawing comparison between traditional growth strategies and the leaf-wise strategy, it must be admitted that this approach is considerably more efficient than the others. What makes the leaf-wise strategy more efficient than the alternative level-wise strategy is this fact that the leaves existing in the same layer are properly taken into consideration, which diminish the need for u
https://www.nature.com/articles/s41598-021-04168-w
Modeling of CO2 adsorption capacity by porous metal organic frameworks using advanced decision tree-based models