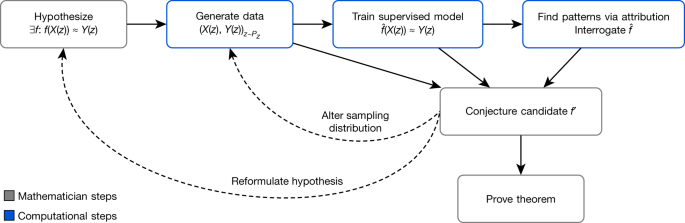
Advancing mathematics by guiding human intuition with AI Alex Davies orcid.org/0000-0003-4917-52341, Petar Veličković1, Lars Buesing1, Sam Blackwell1, Daniel Zheng1, Nenad Tomašev orcid.org/0000-0003-1624-02201, Richard Tanburn1, Peter Battaglia1, Charles Blundell1, András Juhász2, Marc Lackenby2, Geordie Williamson3, Demis Hassabis orcid.org/0000-0003-2812-99171 & Pushmeet Kohli orcid.org/0000-0002-7466-79971 Nature 600, 70–74 (2021)Cite this article Computer sciencePure mathematicsStatistics The practice of mathematics involves discovering patterns and using these to formulate and prove conjectures, resulting in theorems. Since the 1960s, mathematicians have used computers to assist in the discovery of patterns and formulation of conjectures1, most famously in the Birch and Swinnerton-Dyer conjecture2, a Millennium Prize Problem3. Here we provide examples of new fundamental results in pure mathematics that have been discovered with the assistance of machine learning—demonstrating a method by which machine learning can aid mathematicians in discovering new conjectures and theorems. We propose a process of using machine learning to discover potential patterns and relations between mathematical objects, understanding them with attribution techniques and using these observations to guide intuition and propose conjectures. We outline this machine-learning-guided framework and demonstrate its successful application to current research questions in distinct areas of pure mathematics, in each case showing how it led to meaningful mathematical contributions on important open problems: a new connection between the algebraic and geometric structure of knots, and a candidate algorithm predicted by the combinatorial invariance conjecture for symmetric groups4. Our work may serve as a model for collaboration between the fields of mathematics and artificial intelligence (AI) that can achieve surprising results by leveraging the respective strengths of mathematicians and machine learning. One of the central drivers of mathematical progress is the discovery of patterns and formulation of useful conjectures: statements that are suspected to be true but have not been proven to hold in all cases. Mathematicians have always used data to help in this process—from the early hand-calculated prime tables used by Gauss and others that led to the prime number theorem5, to modern computer-generated data1,5 in cases such as the Birch and Swinnerton-Dyer conjecture2. The introduction of computers to generate data and test conjectures afforded mathematicians a new understanding of problems that were previously inaccessible6, but while computational techniques have become consistently useful in other parts of the mathematical process7,8, artificial intelligence (AI) systems have not yet established a similar place. Prior systems for generating conjectures have either contributed genuinely useful research conjectures9 via methods that do not easily generalize to other mathematical areas10, or have demonstrated novel, general methods for finding conjectures11 that have not yet yielded mathematically valuable results.AI, in particular the field of machine learning12,13,14, offers a collection of techniques that can effectively detect patterns in data and has increasingly demonstrated utility in scientific disciplines15. In mathematics, it has been shown that AI can be used as a valuable tool by finding counterexamples to existing conjectures16, accelerating calculations17, generating symbolic solutions18 and detecting the existence of structure in mathematical objects19. In this work, we demonstrate that AI can also be used to assist in the discovery of theorems and conjectures at the forefront of mathematical research. This extends work using supervised learning to find patterns20,21,22,23,24 by focusing on enabling mathematicians to understand the learned functions and derive useful mathematical insight. We propose a framework for augmenting the standard mathematician’s toolkit with powerful pattern recognition and interpretation methods from machine learning and demonstrate its value and generality by showing how it led us to two fundamental new discoveries, one in topology and another in representation theory. Our contribution shows how mature machine learning methodologies can be adapted and integrated into existing mathematical workflows to achieve novel results.A mathematician’s intuition plays an enormously important role in mathematical discovery—’It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems’25. The following framework, illustrated in Fig. 1, describes a general method by which mathematicians can use tools from machine learning to guide their intuitions concerning complex mathematical objects, verifying their hypotheses about the existence of relationships and helping them understand those relationships. We propose that this is a natural and empirically productive way that these well-understood techniques in statistics and machine learning can be used as part of a mathematician’s work.Fig. 1: Flowchart of the framework.The process helps guide a mathematician’s intuition about a hypothesized function f, by training a machine learning model to estimate that function over a particular distribution of data PZ. The insights from the accuracy of the learned function (hat{f}) and attribution techniques applied to it can aid in the understanding of the problem and the construction of a closed-form f′. The process is iterative and interactive, rather than a single series of steps.Concretely, it helps guide a mathematician’s intuition about the relationship between two mathematical objects X(z) and Y(z) associated with z by identifying a function (hat{f}) such that (hat{f})(X(z)) ≈ Y(z) and analysing it to allow the mathematician to understand properties of the relationship. As an illustrative example: let z be convex polyhedra, X(z) ∈ ({{mathbb{Z}}}^{2}times {{mathbb{R}}}^{2}) be the number of vertices and edges of z, as well as the volume and surface area, and Y(z) ∈ ℤ be the number of faces of z. Euler’s formula states that there is an exact relationship between X(z) and Y(z) in this case: X(z) · (−1, 1, 0, 0) + 2 = Y(z). In this simple example, among many other ways, the relationship could be rediscovered by the traditional methods of data-driven conjecture generation1. However, for X(z) and Y(z) in higher-dimensional spaces, or of more complex types, such as graphs, and for more complicated, nonlinear (hat{f}), this approach is either less useful or entirely infeasible.The framework helps guide the intuition of mathematicians in two ways: by verifying the hypothesized existence of structure/patterns in mathematical objects through the use of supervised machine learning; and by helping in the understanding of these patterns through the use of attribution techniques.In the supervised learning stage, the mathematician proposes a hypothesis that there exists a relationship between X(z) and Y(z). By generating a dataset of X(z) and Y(z) pairs, we can use supervised learning to train a function (hat{f}) that predicts Y(z), using only X(z) as input. The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned given a sufficient amount of data. If (hat{f}) is more accurate than would be expected by chance, it indicates that there may be such a relationship to explore. If so, attribution techniques can help in the understanding of the learned function (hat{f}) sufficiently for the mathematician to conjecture a candidate f′. Attribution techniques can be used to understand which aspects of (hat{f}) are relevant for predictions of Y(z). For example, many attribution techniques aim to quantify which component of X(z) the function (hat{f}) is sensitive to. The attribution technique we use in our work, gradient saliency, does this by calculating the derivative of outputs of (hat{f}), with respect to the inputs. This allows a mathematician to identify and prioritize aspects of the problem that are most likely to be relevant for the relationship. This iterative process might need to be repeated several times before a viable conjecture is settled on. In this process, the mathematician can guide the choice of conjectures to those that not just fit the data but also seem interesting, plausibly true and, ideally, suggestive of a proof strategy.Conceptually, this framework provides a ‘test bed for intuition’—quickly verifying whether an intuition about the relationship between two quantities may be worth pursuing and, if so, guidance as to how they may be related. We have used the above framework to help mathematicians to obtain impactful mathematical results in two cases—discovering and proving one of the first relationships between algebraic and geometric invariants in knot theory and conjecturing a resolution to the combinatorial invariance conjecture for symmetric groups4, a well-known conjecture in representation theory. In each area, we demonstrate how the framework has successfully helped guide the mathematician to achieve the result. In each of these cases, the necessary models can be trained within several hours on a machine with a single graphics processing unit.Low-dimensional topology is an active and influential area of mathematics. Knots, which are simple closed curves in ({{mathbb{R}}}^{3}), are one of the key objects that are studied, and some of the subject’s main goals are to classify them, to understand their properties and to establish connections with other fields. One of the principal ways that this is carried out is through invariants, which are algebraic, geometric or numerical quantities that are the same for any two equivalent knots. These invariants are derived in many different ways, but we focus on two of the main categories: hyperbolic invariants and algebraic invariants. These two types of invariants are derived from quite different mathematical disciplines, and so it is of considerable interest to establish connections between them. Some examples of these invariants for small knots are shown in Fig. 2. A notable example of a conjectured connection is the volume conjecture26, which proposes that the hyperbolic volume of a knot (a geometric invariant) should be encoded within the asymptotic behaviour of its coloured Jones polynomials (which are algebraic invariants).Fig. 2: Examples of invariants for three hyperbolic knots.We hypothesized that there was a previously undiscovered relationship between the geometric and algebraic invariants.Our hypothesis was that there exists an undiscovered relationship between the hyperbolic and algebraic invariants of a knot. A supervised learning model was able to detect the existence of a pattern between a large set of geometric invariants and the signature σ(K), which is known to encode important information about a knot K, but was not previously known to be related to the hyperbolic geometry. The most relevant features identified by the attribution technique, shown in Fig. 3a, were three invariants of the cusp geometry, with the relationship visualized partly in Fig. 3b. Training a second model with X(z) consisting of only these measurements achieved a very similar accuracy, suggesting that they are a sufficient set of features to capture almost all of the effect of the geometry on the signature. These three invariants were the real and imaginary parts of the meridional translation μ and the longitudinal translation λ. There is a nonlinear, multivariate relationship between these quantities and the signature. Having been guided to focus on these invariants, we discovered that this relationship is best understood by means of a new quantity, which is linearly related to the signature. We introduce the ‘natural slope’, defined to be slope(K) = Re(λ/μ), where Re denotes the real part. It has the following geometric interpretation. One can realize the meridian curve as a geodesic γ on the Euclidean torus. If one fires off a geodesic γ⊥ from this orthogonally, it will eventually return and hit γ at some point. In doing so, it will have travelled along a longitude minus some multiple of the meridian. This multiple is the natural slope. It need not be an integer, because the endpoint of γ⊥ might not be the same as its starting point. Our initial conjecture relating natural slope and signature was as follows.Fig. 3: Knot theory attribution.a, Attribution values for each of the input X(z). The features with high values are those that the learned function is most sensitive to and are probably relevant for further exploration. The 95% confidence interval error bars are across 10 retrainings of the model. b, Example visualization of relevant features—the real part of the meridional translation against signature, coloured by the longitudinal translation.Conjecture: There exist constants c1 and c2 such that, for every hyperbolic knot K,$$|2sigma (K)-{rm{slope}}(K)| < {c}_{1}{rm{vol}}(K)+{c}_{2}$$While this conjecture was supported by an analysis of several large datasets sampled from different distributions, we were able to construct counterexamples using braids of a specific form. Subsequently, we were able to establish a relationship between slope(K), signature σ(K), volume vol(K) and one of the next most salient geometric invariants, the injectivity radius inj(K) (ref. 27).Theorem: There exists a constant c such that, for any hyperbolic knot K,$$|2sigma (K)-{rm{slope}}(K)|le c{rm{vol}}(K){rm{inj}}{(K)}^{-3}$$It turns out that the injectivity radius tends not to get very small, even for knots of large volume. Hence, the term inj(K)−3 tends not to get very large in practice. However, it would clearly be desirable to have a theorem that avoided the dependence on inj(K)−3, and we give such a result that instead relies on short geodesics, another of the most salient features, in the Supplementary Information. Further details and a full proof of the above theorem are available in ref. 27. Across the datasets we generated, we can place a lower bound of c ≥ 0.23392, and it would be reasonable to conjecture that c is at most 0.3, which gives a tight relationship in the regions in which we have calculated.The above theorem is one of the first results that connect the algebraic and geometric invariants of knots and has various interesting applications. It directly implies that the signature controls the non-hyperbolic Dehn surgeries on the knot and that the natural slope controls the genus of surfaces in ({{mathbb{R}}}_{+}^{4}) whose boundary is the knot. We expect that this newly discovered relationship between natural slope and signature will have many other applications in low-dimensional topology. It is surprising that a simple yet profound connection such as this has been overlooked in an area that has been extensively studied.Representation theory is the theory of linear symmetry. The building blocks of all representations are the irreducible ones, and understanding them is one of the most important goals of representation theory.
https://www.nature.com/articles/s41586-021-04086-x
Advancing mathematics by guiding human intuition with AI