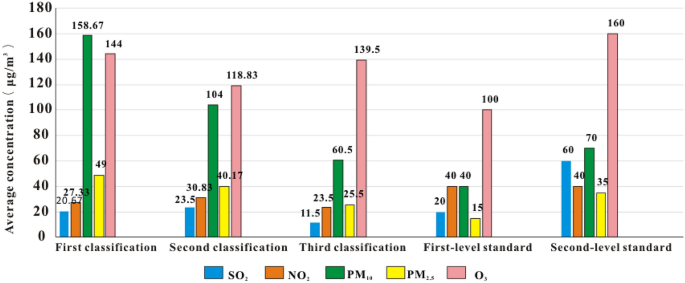
A new method for evaluating air quality using an ideal grey close function cluster correlation analysis method To scientifically and reasonably evaluate air quality with a large amount of monitored data, this paper proposes a new evaluation method called ideal grey close function cluster correlation analysis (IGCFCCA). Taking the air quality in Ningxia Province, China, as an example, according to China’s air quality standard, SO2, NO2, PM10, PM2.5 and O3 are selected as evaluation indexes to perform the evaluation. The results show that the air quality in this region in 2018 can be divided into three classifications, among which the relatively poor air quality in March, April and May is the first classification, the better air quality in August and September is the third classification, and the air quality in other months falls under the second classification. Correlation analysis is used to qualitatively determine that these three classifications correspond to first-level air quality in China’s air quality standard, and the correlation degree, which is the distance between the three classifications and the first-level air quality, is quantitatively determined. Specifically, the correlation degrees of the first-classification, second-classification and third-classification of air quality are 0.674, 0.697 and 0.71, respectively. The research results indicate potential directions and objectives for air quality management to achieve scientific management. The air environment is a dynamic and complex system. The air quality is influenced by some pollutants, such as SO2, NO2, PM10, and O3. The concentrations of these pollutants are changing constantly. However, the monitored data used in analyses are usually collected in a certain period, and examples include one-hour average, few-hour average, one-month average and one-year average data. Instantaneous data collected every minute or second are difficult to collect and analyse. Therefore, this collection approach is considered a grey system. In a grey system, some information is known, and some information is unknown1,2,3,4,5,6,7.At present, China’s air quality standard (GB3095-2012) divides air quality into two levels and stipulates the concentrations of pollutants in first-level and second-level air8,9. The concentrations of pollutants are comparatively lower in first-level air, and they are higher in second-level air. The major pollutants include SO2, NO2, PM10, O3, and others. However, when people evaluate air quality according to GB3095-2012, there may be some problems. First, according to the national standard, the common evaluation methods can only determine which level the current air is associated with. However, there is no analysis of how much the current air belongs to the level, and it is not clear how far the current air is from the standard level. The space for improving the current air quality is also very vague. It is necessary to develop a method to quantitatively calculate the correlation degree, which is the distance between the current air and the two levels of air standards. Second, to determine the air quality in a certain area in a period of time, the concentrations of pollutants are usually monitored every day. However, the amount of monitored data is very large. Obviously, if people compare and analyse each recorded value, the workload will be very large, and tasks will be almost impossible to complete. Therefore, people usually calculate the average value of the data first and then analyse the average. However, among so many monitored data, which data should be taken as a group for average calculation is a problem. In other words, determining how to scientifically classify data is the key. Data with similar characteristics can be classified into one group. These different classifications can be analysed and evaluated. Therefore, the results of the analysis can be scientific.At present, there are many methods for comprehensively evaluating atmospheric environmental quality, including the air pollution index (API) method, ambient air quality index (AQI) method, single factor index method, green air pollution comprehensive index method, analytic hierarchy process, artificial neural network models, and fuzzy comprehensive evaluation method8. Due to the different evaluation principles of various evaluation methods, each method has unique advantages and disadvantages. Among them, the API and AQI methods are simple, intuitive and convenient to use but only applicable for evaluating the short-term air quality in cities9. The single factor index method is clear and easy to implement, but it cannot consider the air quality status as a whole, and the evaluation results are one dimensional9. Green’s comprehensive air pollution index method is easy to understand and implement, but it is only applicable to areas where coal pollution is the main pollution type9. The analytical hierarchy process (AHP) is simple, practical and systematic, but quantitative results are limited; additionally, when there are many indicators, the statistics will be complex, and weights will be difficult to determine9. The artificial neural network evaluation method has the advantages of a fast operation speed, self-adaptation and strong fault tolerance, but the disadvantage is that when the data are poorly correlated, the evaluation results will exhibit homogenization phenomena10,11,12,13. IGCFCCA is a kind of fuzzy comprehensive evaluation method based on fuzzy mathematics, the fuzzy principle and the grey close function. The method can solve the common incomplete data problem and mainly assesses the relationships between uncertainty and incomplete information analysis, model building and forecasting. The method only needs a small amount of data and can achieve good prediction results.In this paper, the IGCFCCA method is used to evaluate the air quality in Ningxia Province. The method can not only scientifically classify a large amount of data but also calculate the correlation degree between each classification and the relevant standard. This approach can provide an important basis for comprehensive environmental management. Moreover, this new method provides a scientific reference and an important basis for the establishment and optimization of other industry standards in the future.A sample, which comes from the monitored data reports of some environmental management departments, is first classified by ideal grey close function cluster analysis. Then, the level of the sample is determined by grey correlation analysis, and comprehensive evaluation conclusions are established according to the correlation degree between the classification of the sample and the levels specified in GB3095-2012.The classification of the sample to be evaluatedEstablishing the evaluation index sequence matrix for the selected sampleLet S be a sequence of clustering objects, i.e., S = {s1, s2…, sm}; X is a sequence of air-influencing variables, i.e., X = {x1, x2…, xn}; xik is the original monitoring data for si (i = 1, 2…, m) and xk (k = 1, 2…, n); i and m represent the number of objects considered in clustering; k and n are the number of the influencing indexes which are the pollutants mentioned above. Accordingly, the following matrix can be established (Eq. 1).$$ S = begin{array}{*{20}c} {s_{1} } \ {s_{2} } \ ldots \ {s_{m} } \ end{array} left[ {begin{array}{*{20}c} {x_{11} } & {x_{12} } & ldots & {x_{1n} } \ {x_{21} } & {x_{22} } & ldots & {x_{2n} } \ ldots & ldots & ldots & ldots \ {x_{m1} } & {x_{m2} } & ldots & {x_{mn} } \ end{array} } right] $$Establishing the matrix of ideal-value grey close function clustersLet X0 = {x01, x02…, x0n} be the ideal-value sequence corresponding to each influential index. The principle for determining the ideal value is as follows (Eqs. 2, 3, 4).The first situation: The larger the influencing index (xk) is, the better the air quality is; in this case, the ideal value$$ x_{0k} = max left{ {x_{ik} ,i = 1,2, ldots ,m} right},k = 1,2, ldots ,n. $$The second situation: The smaller the influencing index (xk) is, the better the air quality is; in this case, the ideal-value$$ x_{0k} = min left{ {x_{ik} ,i = 1,2, ldots ,m} right},k = 1,2, ldots ,n. $$Third, the air quality is best when the influencing index (xk) displays a moderate value, and the ideal value is$$ x_{0k} = {text{M}}. $$According to the ideal value x0k (Eqs. 2, 3 or Eq. 4) and the original monitored data (xik), the grey close function value yik is calculated by using (Eq. 5).$$ y_{ik} = frac{{x_{ok} }}{{x_{ik} }};left( {i = 1,2, ldots ,m;k = 1,2, ldots ,n} right) $$where xik is the original monitored data and x0k is the ideal value corresponding to the k-th influential index. Moreover, the function value yik is dimensionless, and yik ∈ [0,1]. yik denotes the correlation degree of si and s0 for the k-th index. Specifically, the larger yik is, the closer si is to the ideal value s0, and the smaller yik is, the farther si is from s0.Thus, the following grey close matrix Y can be established (Eq. 6).$$ Y = left[ {begin{array}{*{20}c} {y_{11} } & {y_{12} } & ldots & {y_{1n} } \ {y_{21} } & {y_{22} } & ldots & {y_{2n} } \ begin{gathered} ldots hfill \ y_{m1} hfill \ end{gathered} & begin{gathered} ldots hfill \ y_{m2} hfill \ end{gathered} & begin{gathered} ldots hfill \ ldots hfill \ end{gathered} & begin{gathered} ldots hfill \ y_{mn} hfill \ end{gathered} \ {y_{01} } & {y_{02} } & {…} & {y_{0n} } \ end{array} } right] $$In this case, Y is the grey close function value. Moreover, (y01, y02…, y0n) = (1,1…,1)1×n is the ideal sequence, and the bigger yik is, the better si is; the biggest yik is equal to 1.The classification of the sample to be evaluatedBecause the influence of each influencing index is different, the weight of each influencing index needs to be considered. Let Pi be the comprehensive analysis value of si. Pi can be expressed as follows (Eq. 7)$$ P_{i} = sumlimits_{k = 1}^{n} {Wy_{ik} } left( {i = 1,2 ldots ,m} right) $$where W is the weight of each influencing index, and since the number of indexes is k, the number of W values is also k (W1, W2…, Wk). Corresponding, the following equation can be established (Eq. 8).$$ W_{k} = frac{{sumlimits_{i = 1}^{m} {X_{{i{text{k}}}} } }}{{sumlimits_{i = 1}^{m} {sumlimits_{k = 1}^{n} {X_{ik} } } }};left( {k = 1,2 ldots ,n} right) $$Based on the actual comprehensive analysis value Pi, Pj = (P1, P2…, Pm)T. The following equation (Eq. 9) can be used to calculate the grey close value Pij of Pi in relation to Pj.$$ P_{ij} = frac{{min (p_{i} ,p_{j} )}}{{max (p_{i} ,p_{j} )}};left( {i,j = 1,2 ldots ,m} right) $$Then,$$ P = left( {P_{ij} } right)_{m times m} . $$If P (Eq. 10) satisfies the following three conditions: (1) reflexivity, where Pij = 1 (i = j); (2) symmetry, where Pij = Pji; and (3) normativity, where Pij ∈ [0,1], we can select the appropriate threshold value from the P matrix, intercept the branches with weight values less than λ, which is the similarity coefficient4,5, and establish the classification (S_{t}^{prime }) (t = 1, 2…, c) when λ level meets the relevant requirement. (S_{t}^{prime }) represents each classification of the air in a given region. The following equations (Eqs. 11, 12) can be established.$$ S_{t}^{prime } = left( {S_{1}^{prime } ,S_{2}^{prime } ldots ,S_{c}^{prime } } right)^{{text{T}}} $$$$ S_{tk}^{prime } = left( {S_{t1}^{prime } ,S_{t2}^{prime } ldots ,S_{tn}^{prime } } right) $$where (S_{t}^{prime }) is the t-th classification, (S_{tk}^{prime }) is the kth index of the t-th classification, t is the number of classifications, and k is the number of influencing indexes.(S_{tk}^{prime }) can be expressed in the following matrix form (Eq. 13).$$ S_{tk}^{prime } = left[ {begin{array}{*{20}c} {s_{11}^{prime } } & {s_{12}^{prime } } & ldots & {s_{1n}^{prime } } \ {s_{21}^{prime } } & {s_{22}^{prime } } & ldots & {s_{2n}^{prime } } \ ldots & ldots & ldots & ldots \ {s_{cc}^{prime } } & {s_{c2}^{prime } } & ldots & {s_{cn}^{prime } } \ end{array} } right] $$Correlation degree analysis of the sample to be evaluatedLet (S_{t}^{prime }) be the sample to be evaluated, and let X = (x1, x2…, xn), which is the influencing index set mentioned above and is the evaluation index used for (S_{t}^{prime }). Let ({text{S}}_{0}^{prime }) be the stated air quality classification in the GB3095-2012. Then, the equation for the correlation coefficient is as follows (Eq. 14)14.$$ zeta_{t} (k) = frac{{mathop {min }limits_{t in c} mathop {min }limits_{k in n} left| {S_{t}^{prime } (k) – {text{S}}_{0}^{prime } (k)} right| + epsilon mathop {max }limits_{t in c} mathop {max }limits_{k in n} left| {S_{t}^{prime } (k) – {text{S}}_{0}^{prime } (k)} right|}}{{left| {S_{t}^{prime } (k) – {text{S}}_{0}^{prime } (k)} right| + epsilon mathop {max }limits_{t in c} mathop {max }limits_{k in n} left| {S_{t}^{prime } (k) – {text{S}}_{0}^{prime } (k)} right|}} $$where ζt (k) is the correlation coefficient and ε is the resolution coefficient, with a general value of 0.54,5.Moreover, the correlation degree (Rt) equation is as follows (Eq. 15).$$ R_{t} = frac{1}{n}sumlimits_{k = 1}^{n} {zeta_{t} } (k) $$The value of Rt is calculated by using (Eq. 15). The maximum value of Rt indicates that the sample to be evaluated has the highest correlation degree with the considered air quality level. Therefore, the sample is classified correspondingly.Monthly reports of the air quality in Ningxia Province in 2018 were provided by the Department of Ecology and Environment of Ningxia Province. The monthly report data were used to establish the cluster of samples S (Table 1) (Eq. 1). Each sample included five kinds of pollutants. Moreover, the concentrations of SO2, NO2, PM10 and PM2.5 were based on monthly averages calculated from 24-h averages, and the concentration of O3 was the monthly average calculated from the 8-h average values.Table 1 Air quality in Ningxia Province in 2018.x1 is the SO2 concentration; x2 is the NO2 concentration; x3 is the PM10 concentration; x4 is the PM2.5 concentration; and x5 is the O3 concentration. For these pollutants, the lower the concentration is, the better the air quality is.As shown in Table 1, because the management department only provided some monitored data and the data in January are incomplete, only the data that are listed in the table from February to December can be effectively analysed. However, the focus of this study is on the new analysis and evaluation method (IGCFCCA), and almost all of the data can be analysed by this method.According to (Eq. 3), the five ideal values are as follows: x01 is 9, x02 is 17, x03 is 56, x04 is 25, and x05 is 76. Based on the sample data in Table 1, the ideal-value grey close matrix (Eq. 6) can be obtained from (Eq. 5); according to (Eq. 8), the weights of x1, x2, x3, x4 and x5 are w1 = 0.06, w2 = 0.09, w3 = 0.34, w4 = 0.12, and w5 = 0.39, respectively. Consequently, the comprehensive analysis value Pi (i = 1, 2…, 11) (Table 2) of Si is calculated with (Eq. 7). The grey close function value yik (Eq. 5) and the comprehensive analysis value Pi are shown in Table 2.Table 2 Grey close function value and the comprehensive analysis value.With Pi (P1, P2… and P11) as known numbers, Pij (j = 1, 2…, 11) can be calculated from (Eq. 9). The corresponding elements of the grey similar matrix (Eq. 10) are shown in Table 3.Table 3 Grey close values Pij.The following information can be obtained from Table 3. If λ = 0.94,5, S2, S3 and S4 correspond to the first classification (S_{1}^{prime }); S7 and S8 correspond to the third classification (S_{3}^{prime }); and the other S values correspond to the second classification (S_{2}^{prime }). S2, S3 and S4 are the samples for March, April and May, respectively, and S7 and S8 are the samples for Augus
https://www.nature.com/articles/s41598-021-02880-1
A new method for evaluating air quality using an ideal grey close function cluster correlation analysis method