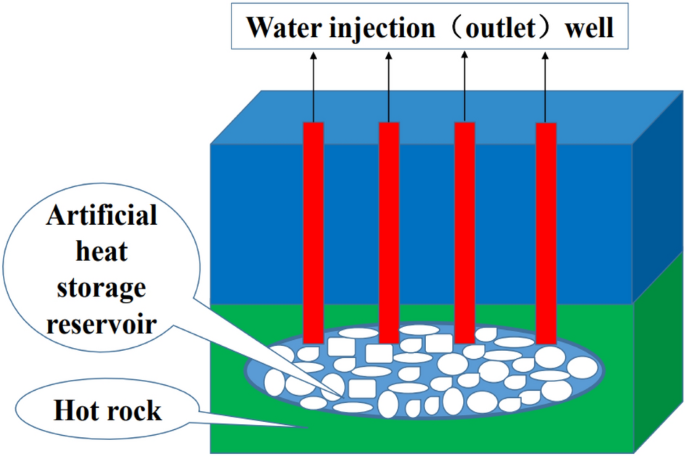
A new mathematical modeling approach for thermal exploration efficiency under different geothermal well layout conditions The water temperature at the outlet of the production well is an important index for evaluating efficient geothermal exploration. The arrangement mode of injection wells and production wells directly affects the temperature distribution of the production wells. However, there is little information about the effect of different injection and production wells on the temperature field of production wells and rock mass, so it is critical to solve this problem. To study the influence mechanism of geothermal well arrangement mode on thermal exploration efficiency, the conceptual model of four geothermal wells is constructed by using discrete element software, and the influence law of different arrangement modes of four geothermal wells on rock mass temperature distribution is calculated and analyzed. The results indicated that the maximum water temperature at the outlet of the production well was 84.0 °C due to the thermal superposition effect of the rock mass between the adjacent injection wells and between the adjacent production wells. Inversely, the minimum water temperature at the outlet of the production well was 50.4 °C, which was determined by the convection heat transfer between the water flow and the rock between the interval injection wells and the interval production wells. When the position of the model injection well and production well was adjusted, the isothermal number line of rock mass was almost the same in value, but the direction of water flow and heat transfer was opposite. The study presented a novel mathematical modeling approach for calculating thermal exploration efficiency under various geothermal well layout conditions. In the process of geothermal exploration, if the limited groundwater resources around the geothermal well cannot replenish pumping capacity through runoff, it is then necessary to consider the injection well. This is replenish production well-pumping capacity in time to achieve the dynamic balance between pumping capacity and injection capacity, allowing for long-term geothermal exploration. Underground hot water can be used for heating and generating power after being pumped to the ground. The geothermal water extraction system is affected not only by the groundwater flow field and temperature field but also by the layout of geothermal wells and many other factors. Under the combined effect of these factors, how injection wells and production wells are scientifically and reasonably arranged has a significant impact on the temperature field of the rock mass near the production wells and well groups. Therefore it is of great engineering significance to study the wellbore temperature field in the exploration and development of geothermal resources1,2,3.At present, research on geothermal well temperatures primarily focuses on numerical simulation analysis. Many scholars have researched the influencing factors of fluid, rock temperature field and wellbore temperature4, the influence of groundwater flow velocity in sandy aquifer on the thermal performance of borehole heat exchanger5, three-dimensional thermoporoelastic modeling and analysis of flow, heat transport and deformation in fractured rock with applications to a lab-scale geothermal system6 and numerical simulation analysis on the influence of different factors on the thermal distribution around wellbore7. Groundwater flow estimation for temperature monitoring in borehole heat exchangers during thermal response tests8, heat extraction analysis of a novel multilateral-well coaxial closed-loop geothermal system9 and research on the influence of borehole heat-water exchanger characteristics on the performance of vertical closed-loop ground heat pump systems were carried out10. Gao11,12 studied the influence mechanism of geothermal well spacing, geothermal temperature and production well depth on the water flow and heat transfer temperature of rock masses, but the literature did not consider the influence of the interaction of injection wells and production wells on the temperature field of production wells and rock masses. Research on outlet temperature and temperature field of geothermal well13,14,15,16, sensitivity analysis of influencing factors for heat loss of geothermal wells17 and wellbore temperature loss model and application for heating geothermal mining18. However, the research contents of these scholars did not involve the comparative study of the water temperature and temperature field at the outlet of geothermal wells under different conditions of the water inlet and water outlet. Scholars have carried out researches on the influence of pumping and irrigation well layout on the groundwater flow field and temperature field19, the influence of pumping and irrigation well distribution mode, and pumping and irrigation well water quantity on heat transfer characteristics of underground heat exchanger well20,21, and the application of numerical simulation of water and heat transport to optimize pumping and irrigation well the layout of groundwater source heat pump system22, numerical simulation of water-heat coupling of single well ground water source heat pump in T2Well23 and optimization of reasonable well spacing and layout of shallow source heat pump simulated by sand tank-taking Jiuxi in Fenglin as an example24. Sustainable electricity generation from an enhanced geothermal system were carried out considering reservoir heterogeneity and water losses with a discrete fracture model25 and enhanced geothermal systems (EGS): hydraulic fracturing in a thermoporoelastic framework26 and modified zipper fracturing in an enhanced geothermal system reservoir and heat extraction optimization via orthogonal design27. Again, Xu et al.28 Studied on optimal arrangement of pumping and irrigation systems for a groundwater heat pump. Deng et al.29 conducted a simulation study on the optimization of middle-deep geothermal recharge wells based on optimal recharge efficiency. Olabi et al.30 thought that geothermal-based hybrid energy systems are an energy method towards eco-friendliness. Rezaei et al.31 researched an enviro-economic optimization of a hybrid energy system from biomass and geothermal resources for low-enthalpy areas. The system off-design evaluation of geothermal-solar hybrid power and operational strategies for its heat pump system was studied32,33. Tian et al.34 studied Carbon–neutral hybrid energy systems with deep water source cooling, biomass heating, and geothermal heat and power. Chen et al.35 carried out Thermodynamic performance analysis and multi-criteria optimization of a hybrid combined heat and power system coupled with geothermal energy. In summary, although some achievements have been made in the study of geothermal well temperature, there are few reports on the complex model of thermal recovery efficiency optimization under different geothermal well layout conditions. The actual geothermal mining process is closely related to the scientific and reasonable layout of geothermal wells. The influence of different geothermal well layout conditions on the temperature field of production wells and rock masses is directly related to the safety and efficiency of geothermal mining. Given this, it is necessary to research the optimization of thermal mining efficiency under different geothermal well layout conditions.In this paper, first, the fractured rock mass models of four injection wells and production wells are constructed by 3DEC discrete element software. The effect of different water inlets and outlets on the temperature field of the production well and rock mass, as well as the water temperature of the production well outlet, is then calculated under various geothermal well layout conditions. Finally, through comparative analysis, the law of the influence of different geothermal well layouts on the rock mass water flow and heat transfer temperature is revealed.Figure 1 shows a schematic diagram of geothermal resource exploitation. Four water injection wells and water output wells were drilled from the ground by using mechanical drills. The hot rock area at the bottom of the water injection wells and water output wells was mechanically fractured to form a microjoint system to open its fractured channel. The ground injected low-temperature water into the water injection well, and the water flowed into the well’s bottom. Hot water is stored in the artificial heat reservoir area through convection and heat transfer with high-temperature hot rock, and high-temperature water is pumped out to the ground through the well for comprehensive utilization, such as power generation and heat. In this paper, only four injection wells and production wells are considered, and engineering fracture systems are ignored.Figure 1Schematic diagram of geothermal resource exploitation.The variables involved in heat conduction in 3DEC are temperature and the three components of the heat flux. The energy balance equation and Fourier law of heat conduction are related to these variables. The differential equation of heat conduction is obtained by combining the Fourier law with the energy balance equation. The differential equation can be solved under specific boundary and initial conditions based on specific geometry and properties. The following dimensionless numbers are used to characterize transient heat conduction.Characteristic length:$$Lc = frac{{V_{s} }}{{A_{s} }}$$where the characteristic length of the solid is expressed by (Lc)[m]; the volume of the solid is expressed by (V_{s})[m3], and the surface area of heat exchange is expressed by (A_{s})[m2].Thermal diffusivity:$$kappa = frac{k}{{rho C_{v} }}$$where (kappa) is the thermal diffusivity in [m2/s]; k is the thermal conductivity in [W/(m·°C)]; ρ is the density in [kg/m3]; and Cv is the specific heat at constant volume in [J/kg·°C].Characteristic time:$$t_{c} = frac{{L_{C}^{2} }}{kappa }$$where the characteristic time of the solid is expressed by (t_{c})[s].The differential expression of the energy balance has the following form:$$- q_{i,i} + q_{v} = frac{partial zeta }{{partial t}}$$where qi,i is the heat-flux vector in [W/m3]; qv is the volumetric heat-source intensity in [W/m3], and ζ is the heat stored per unit volume in [J/m3].In general, the temperature change may be caused by variations in both energy storage and volumetric strain ε. The constitutive thermal law relating those parameters may be expressed.as:$$frac{partial T}{{partial t}} = M_{th} (frac{partial zeta }{{partial t}}{ – }beta_{th} frac{partial varepsilon }{{partial t}})$$where Mth and βth are material constants and T represents the temperature.In this law, a particular case of βth = 0 and Mth = (frac{{1}}{{rho C_{v} }}) is considered, in which ρ is the mass density of the medium in [kg/m3] and Cv is the specific heat at constant volume in [J/kg·°C]. The change in strain is assumed to play a minor role in influencing the temperature validity for quasistatic mechanical problems involving solids and liquids.$$frac{partial zeta }{{partial t}} = rho C_{v} frac{partial T}{{partial t}}$$By substituting Eq. (6) for Eq. (4), the energy-balance equation was yielded.$$- q_{i,i} + q_{v} = rho C_{v} frac{partial T}{{partial t}}$$For all solids and liquids, the specific heats at constant pressure and constant volume are principally equivalent. Accordingly, Cv and Cp can be used by each other.According to the finite-difference approximation principle of spatial derivatives, the numbers from 1 to 4 represent each node of the tetrahedron, the opposite side of node n is face n, and the value of the superscript (f) is related to the relevant variable on the face f.The temperature changes linearly in the tetrahedron. The temperature gradient is represented by the node value of temperature according to the Gauss divergence theorem:$$T,_{j} = – frac{1}{3V}mathop sum limits_{l = 1}^{4} T^{l} n_{j}^{(l)} S^{(l)}$$where the external unit vector perpendicular to surface l is denoted by [n](l), the surface area is denoted by S, and the tetrahedral volume is denoted by V.Energy-balance equation formula of nodes. The energy-balance Eq. (7) may be expressed as:where$$b* = rho C_{v} frac{partial T}{{partial t}} – q_{v}$$is the instantaneous “physical strength” in the mechanical node formula. Using a tetrahedron analogy, the nodal heat (Q_{e}^{n} [w]) n = 1,4 in equilibrium with its heat flux and body force can be expressed as:$$Q_{e}^{n} = Q_{t}^{n} { – }frac{{q_{v} V}}{{4}} + m^{n} C_{v}^{n} frac{{{text{d}}T^{n} }}{dt}$$where$$Q_{t}^{n} = frac{{q_{i} n_{i}^{(n)} S^{(n)} }}{3}$$and$$m^{n} = frac{rho V}{{4}}$$In this theory, the node form of the energy-balance equation is required at each global node, in which the sum of equivalent node heat ((- Q_{e}^{n})) of all tetrahedrons and the node contribution ((- Q_{w}^{n})) of the applied boundary flux and source are zero.In heat convection, it is presumed that fluid flow occurs within saturated fractures while the rock matrix is impermeable. As described in the previous section, heat can be transported by fluid convection, conducting in itself, and the rock mass. The fluid temperature generally varies in different rocks. Therefore, between the fracture fluid and the contacting rock (fluid-thermal coupling), heat transfer may occur, according to Newton’s law of cooling. Coupling to heat transfer within the rock and the logic for heat transfer within the fluid is presented as follows.Heat convection in the flow planes is described by the following equations. Heat is transported.by conduction in the fracture fluid, according to Fourier’s law:$$q_{f}^{T} = – k_{f}^{T} Delta T$$where (q_{f}^{T}) is the specific heat flux in the fluid in [W/s2] and (k_{f}^{T}) is the fluid thermal conductivity in [W/(m·°C)]. The energy-balance equation for the fluid obeys the equation.$$rho_{f} c_{f} frac{{partial T_{f} }}{partial t} + nabla cdot q_{f}^{T} + rho_{f} c_{f} q^{f} cdot nabla T_{f} + A_{f} h(T_{f} – T_{s} ) = 0$$where (rho_{f} c_{f}) is the fluid density [kg/m3] times the specific heat [J/(g·°C)]; (q^{f}) is the specific fluid discharge.in [m2/s]; (A_{f}) is the contact area per unit fluid volume in [m2]; h is the fluid/rock heat transfer coefficient in [W/(m2·°C)]; and Tf and Ts are the temperatures of the fluid and solid block, respectively.For the solid blocks, the fluid flow was neglected; the transport of heat obeys Fourier’s law as follows:$$q^{T} = – k^{T} Delta T$$where qT is the specific heat flux in [W/s2] and kT is the rock thermal conductivity in [W/(m·°C)]. The energy balance is$$rho_{s} c_{s} frac{{partial T_{s} }}{partial t} + nabla cdot q_{s}^{T} – A_{s} h(T_{f} – T_{s} ) = 0$$where (rho_{{text{s}}} c_{s}) is the solid density [kg/m3] times the specific heat [J/(g·°C)] and As is the contact area per unit volume of solid (from the aspect of fluid, there is contact on two sides: (A_{s}^{ + }), (A_{s}^{ – }), and As = (A_{s}^{ + }) + (A_{s}^{ – })).In this paper, it is assumed that there is a hot rock with well-developed fractures in Northwest China, which has a huge heat reserve but is relatively deficient in groundwater resources. As a result, it proposed to inject water and effluent to ensure the long-term viability of geothermal exploration and provide stable expedition for local businesses. Considering the hydrothermal heat storage at approximately 100 m underground, low-temperature geothermal resources less than 90 °C are used for heating and technological processes. In the process of geothermal exploration, the interaction between the injection well and production well affects the water temperature distribution at the outlet of the production well and the temperature of the rock mass. The geothermal expedition proc
https://www.nature.com/articles/s41598-021-02286-z
A new mathematical modeling approach for thermal exploration efficiency under different geothermal well layout conditions