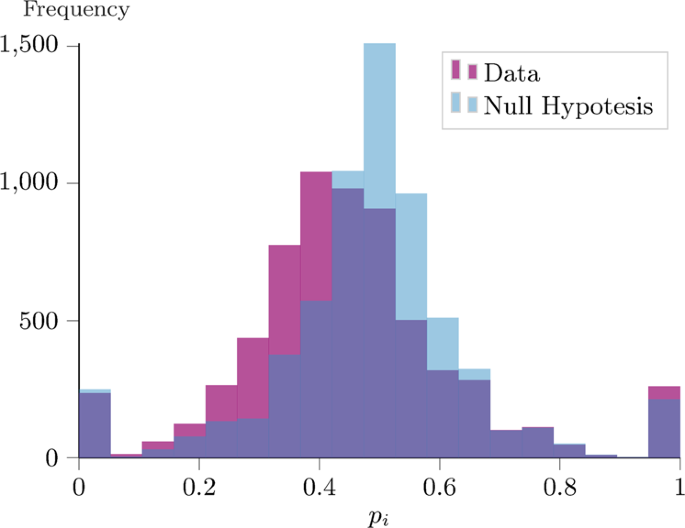
A meritocratic network formation model for the rise of social media influencers Many of today’s most used online social networks such as Instagram, YouTube, Twitter, or Twitch are based on User-Generated Content (UGC). Thanks to the integrated search engines, users of these platforms can discover and follow their peers based on the UGC and its quality. Here, we propose an untouched meritocratic approach for directed network formation, inspired by empirical evidence on Twitter data: actors continuously search for the best UGC provider. We theoretically and numerically analyze the network equilibria properties under different meeting probabilities: while featuring common real-world networks properties, e.g., scaling law or small-world effect, our model predicts that the expected in-degree follows a Zipf’s law with respect to the quality ranking. Notably, the results are robust against the effect of recommendation systems mimicked through preferential attachment based meeting approaches. Our theoretical results are empirically validated against large data sets collected from Twitch, a fast-growing platform for online gamers. Especially since the explosion of online services in the past couple of decades, the impact of social networks on our lives has become more and more multifaceted: they play central roles, e.g., in the dissemination of information1, in the adoption of new technologies2, in the diffusion of healthy behavior3, in the formation and polarization of public opinion4,5. To advance our understanding of the phenomena that take place within these platforms, there has been a recent coming-together of multiple disciplines in the study of social networks. Much of the attention has been devoted to measuring the macroscopic properties of these networks, e.g., degree, density, or connectivity, as well as to understanding the microscopic formation mechanisms6.Along with the rapid research progress, nowadays online social networks are also evolving into new forms. Compared with those that flourished in the first decade of the 21st century, e.g., Facebook and LinkedIn, today’s most popular platforms, such as Twitter, Instagram, or TikTok, exhibit some noticeably distinguishing features. One of the most prominent differences is that these new online social platforms are directed networks that do not require mutual consent for a friendship. As such, the lifeblood of these virtual friendships is the User-Generated Content (UGC)7,8: in 2020, every day 500 million tweets were sent (www.dsayce.com/social-media/tweets-day/), and >80 million Instagram pictures were posted (www.omnicoreagency.com/instagram-statistics/). Thanks to the use of hashtags and integrated search engines, these new social platforms encourage their users to explore the UGC based on their interests. Thereby, users tend to follow real-life strangers and create interest-based communities.The statistical features of the aforementioned directed UGC-based online social platforms are not the same as of real-life social networks. Yet, these directed UGC-based online platforms largely affect our societies in terms of, e.g., public opinion polarization9, or spreading of (mis)information10. Moreover, since these directed platforms increase the possibility to reach wide audiences (way beyond real-life friends), users can now rapidly gain popularity11 through their UGC, and become the so-called new influencers12. This trend has deeply influenced consumers’ and companies’ behavior in markets13 to the point that >70% of US businesses engaged Instagram influencers to promote their products in 2017 (www.emarketer.com).Given the potentially profound impacts of the UGC-based online social platforms on public opinions and economic behavior, as well as the spreading potential of highly influential nodes, it is important to understand (i) how the UGC relates to the emergence of tremendously fast-growing social media influencers, and (ii) what are the properties of the resulting networks.Intuitively, better quality UGC is more likely to attract users because of its higher emotional value14,15. Thus, the network formation process on these platforms depends on a fundamental ingredient, the quality of the UGC. However, except for the fitness model16 in which users are connected with probability proportional to the individuals’ fitness attributes, the large multidisciplinary interest in the study of network formation has so far privileged topological and socio-economic aspects observed in offline social networks (or in online social networks which mimic them, e.g., Facebook) and neglected the effect of the UGC. For example, Stochastic Actor-Oriented Models17, in sociology, and strategic network formation models18, in economics, assume actors decide their ties according to a utilitarian principle based on sociological elements, such as reciprocity or network closure19, or topological measures, e.g., in-degree or closeness centrality20, or a combination of them21. These models typically lead to networks characterized by bilateral social connections and high transitivity. However, on Instagram, only 14% of the relationships are reciprocated and the average clustering coefficient is smaller than 10% (for comparison, on Facebook reciprocity and clustering score, respectively, 100% and 30%)22. Among the random graph models (see the seminal work by Erdös and Rényi23 and see refs. 24,25,26 for extensive surveys), the preferential attachment model, proposed by Barábasi and Albert27, in which newborn nodes choose connections proportional to the degree, has been widely acknowledged. While this mechanism leads to the scale-free effect observed in many real-world networks28, this rich-get-richer philosophy does not justify the rise of new Instagram celebrities, i.e., the so-called Instafamous29, whose success is built without prior fame.The prevalence of directed, UGC-based social networks and the absence of proper mathematical models inspire us to think about their formation processes from an untouched perspective. In this paper, we propose a simple yet predictive network formation mechanism that incorporates both the utilitarian principle and the UGC quality. We assume users have a common interest and we associate them with an attribute defining the quality of their UGC. To define a UGC-based formation process, we collected a longitudinal Twitter data set on network scientists30. Analyzing the temporal sequence of connections, we found evidence that the formation process on directed social networks results from the individuals’ continuous search for better quality UGC, measured by the alignment with the follower’s interests, i.e., homophily31, and its goodness32. Based on this sociological evidence, in our model agents meet with uniform or in-degree-based probability, and strategically create their ties according to a meritocratic principle, i.e., based on the UGC quality. Depending on the application, the model can incorporate users that do not actively contribute with their UGC, e.g., viewers on YouTube.We analytically and numerically study the proposed network formation dynamics as well as the network properties at equilibrium under different meeting probability functions. First, we found that the out-degree distribution has characteristics similar to a gamma distribution, with expectations equal to the harmonic number of the network size. Furthermore, the resulting networks feature real-world social networks’ properties, e.g., small diameter and small, but not vanishing, clustering coefficient, and a significant overlap in the followers’ sets as a result of the homophily that characterizes agents with similar interests. Moreover, the in-degree distribution satisfies the well-known scaling property27, but we also discover a specific pattern: the highest quality node expects to have twice (respectively, three times) as many followers as the second (respectively, third) highest, and so on. This empirical regularity has been found in many systems33 and goes under the name of Zipf’s law34. Notably, this result is robust against the effect of recommendation systems (which increase the visibility of popular nodes). We emphasize that, despite being widely assumed to be ubiquitous for systems where objects grow in size35, the principle underlying the origin of Zipf’s law is an open research question (see ref. 33 for a survey), and our quality-based rule reveals an intuitive, meritocratic mechanism for it. Finally, to empirically validate our model, we collected three data sets36 from Twitch, a popular platform for online gamers (https://www.twitch.tv/p/press-center/). The successful comparison with our theoretical predictions indicates that our model, despite its simple and parsimonious form, already captures several real-world properties.The majority of today’s online social networks offer the users the possibility to actively contribute to the platform’s growth by sharing different forms of UGC, according to their interests, competencies, and willingness. Looking from a different perspective, users are also exposed to the content generated by others on the platform. Thanks to the integrated search engines and the use of hashtags they can explore this content, discover users with similar interests, and ultimately decide to become followers. Given the limited time, they can spend on social media platforms, intuitively users seek to optimize the list of followees so as to receive high-quality content.Meritocratic principleIn order to support our intuition, we collected a longitudinal Twitter data set30 on a network composed of >6000 scientists working in the area of complex social networks. Compared with other data sets, one of the advantages is that we can expect most of the complex network scientists to be active on Twitter, given that they consistently study social networks effects. Moreover, the most popular nodes can be easily associated with renowned researchers in the field. Arguably, the number of followers can be considered as a proxy for the quality of the content generated by a user. We support this hypothesis by manually inspecting and labeling the top in-degree nodes.Then, we enumerate the agents in decreasing in-degree order, so that agent 1 (presumably providing the best UGC) is the most followed, agent 2 is the second most, and so on. For each agent i, we reconstruct the temporal sequence of the outgoing connections (({i}_{1},{i}_{2},ldots ,{i}_{{d}_{i}^{{{{{{{{rm{out}}}}}}}}}})), where ik is the index (rank) of the destination of the k-th outgoing connection of agent i, and ({d}_{i}^{{{{{{{{rm{out}}}}}}}}}) is her final out-degree. Then, for each agent i we compute the probability$${p}_{i}=frac{left|{jin left{2,ldots ,{d}_{i}^{{{{{{{{rm{out}}}}}}}}}right},,{{mbox{s.t.}}}{i}_{j} , > , {{mbox{median}}},{{i}_{1},ldots ,{i}_{j-1}}}right|}{{d}_{i}^{{{{{{{{rm{out}}}}}}}}}-1},$$that estimates the likelihood that a new connection of agent i is higher (in ranking) than the median of the previous connections. At one extreme, for pi = 0 the sequence (({i}_{1},{i}_{2},ldots ,{i}_{{d}_{i}^{{{{{{{{rm{out}}}}}}}}}})) is such that every new followee has a rank smaller than (or equal to) the median of the current list of followees’ ranks, i.e., ({i}_{j}le ,{{mbox{median}}},{{i}_{1},ldots ,{i}_{j-1}}). As such, the rolling median, i.e., the median computed among the first k elements, is always non-increasing in k, and the user is continuously seeking better UGC. Conversely, for pi = 1 the rolling median is always increasing.In Fig. 1 we compare the histogram of the empirical distribution of pi (in purple) with the null hypothesis, plotted in blue, in which we remove the temporal-ordered pattern of the sequence. The elements in agent i’s followees set ({{{{{{{{mathcal{F}}}}}}}}}_{i}^{{{{{{{{rm{out}}}}}}}}}:= {{i}_{1},{i}_{2},ldots ,{i}_{{d}_{i}^{{{{{{{{rm{out}}}}}}}}}}}) are randomly re-ordered: in the new sequence (({bar{i}}_{1},{bar{i}}_{2},ldots ,{bar{i}}_{{d}_{i}^{{{{{{{{rm{out}}}}}}}}}})), the k-th element of the list is drawn uniformly at random from ({{{{{{{{mathcal{F}}}}}}}}}_{i}^{{{{{{{{rm{out}}}}}}}}}setminus left({bar{i}}_{1},ldots ,{bar{i}}_{k-1}right)). The null hypothesis has a median value of ~0.5, which is easy to interpret: if the sequence is completely random, adding an extra element to the partial sequence has a 50% probability of being above the median, and 50% probability of being below it. Comparing the two distributions, we notice that empirical data tend to have a decreasing quality-ranking sequence of followees. As the difference is statistically significant, we can reject the hypothesis that the temporal sequence is random.Fig. 1: Median-rule violation on the Twitter data set.In purple, we plot the histogram of the probability pi as defined in eq. (1). The data refer to N = 6474 agents out of the original 6757 by considering those with an out-degree of at least two. The median of the distribution is 0.436 (mean and std: 0.450, 0.189). In light blue, we compute the same distribution upon reshuffling the temporal sequences of the connections (null hypothesis). The median of this distribution is 0.5 (mean and std: 0.489, 0.173). The two distributions are statistically significantly different (p value of Kolmogorov–Smirnov test ≪ 10−8).Ultimately, this empirical evidence confirms our intuition, i.e., users tend to continuously increase the quality threshold of the new followees. This characteristic, though, is missing in the network formation literature, as there is typically no quality associated with the users. For instance, in the preferential attachment model27, each user selects m followees proportional to their in-degree. If the network is large enough, the probability of selecting a node k in the d-th draw does not depend on d. Therefore, the temporal sequence of connections of the preferential attachment model is similar to the null hypothesis. Moreover, even in the fitness model16 where the quality (fitness) is considered, users tend to connect to high-quality nodes first, rather than later.Quality-based modelTo formalize our quality-based model, we consider the unweighted directed network among N ≥ 2 agents whose UGC revolves around a specific common interest, e.g., a particular traveling destination. We denote the directed tie from i to j with ({a}_{ij}in left{0,1right}), where aij = 1 means i follows j. Then, we assume there are no self-loops and that each agent i can only control her followees aij but not her followers aji. Similarly to the approach in the fitness model16, we endow each actor i with an attribute qi, drawn from a probability distribution, e.g., uniform, normal, exponential di
https://www.nature.com/articles/s41467-021-27089-8
A meritocratic network formation model for the rise of social media influencers